Impact calculation for quantitative risk analysis
Moderator: Intaver Support
-
PetroleumCons
- Posts: 7
- Joined: Tue Feb 20, 2007 10:29 pm
Impact calculation for quantitative risk analysis
I have cost and duration (schedule-related) risks. Could you please explain me how risk impact is calculated?
-
Intaver Support
- Posts: 995
- Joined: Wed Nov 09, 2005 9:55 am
Re: Impact calculation for quantitative risk analysis
We wrote a story to illustrate the calculation algorithm:
Two pirates, Jonny Death and Orlando Plume found that a treasure chest was buried beneath the parking lot of the Miami Dolphin’s Stadium and are planning to dig it out in the morning. However, Captain Barabusa suspects that Jonny and Orlando have discovered something and intends to arrive at the parking lot at exactly the same time. But our two clever pirates have a plan; while Jonny excavates the treasure chest, Orlando will attempt to disorient Barabusa by telling him that Jonny is just sewer repair contractor and send Barabusa off in the wrong direction. As part of their plan, they created a project schedule :
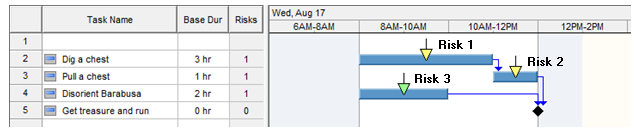
The final question is how Jonny and Orlando are going to the treasure. After some discussion, they decide that who assumes the most risk should receive the largest share of the treasure. They also agree, that most important risk is that which has the potential to cause the greatest delay in the project. They identified 3 risks:
Probability Delay of the task this risk is assigned to
1 Concrete of the parking lot may be stronger than expected: Probability=20% Task Delay=20%
2 The chest will be heavier than expected: Probability=20% Task Delay=20%
3 Captain Barabusa may be smarter than expected and it will take longer to disorient him: Probability=90% Task Delay=80%
Based on this risk breakdown structure, Jonny will have to deal with the first two risks, while Orlando with deal with the last one. Orlando argues that he is assuming the most critical (90% chance that this risk will cause 80% delay) and that he deserves greater share of treasure. If we were performing qualitative analysis, where are not assigned to the project schedule, he would absolutely correct. However, in quantitative analysis that use Monte Carlo simulations, the results can be completely be decidedly different..
In quantitative analysis, the impact of risks are calculated based on the correlation between specific changes in duration, cost, or other parameter caused by the risk occurring and and changes in the overall project duration, cost, or other parameters.
Here is how calculation works in our particular example. In each Monte Carlo simulation, changes in duration caused by particular risk are calculated. For example, in simulation 1 due to the risk “Concrete of the parking lot may be stronger than expected” Task 1 experiences a delay of 0.6 hours.
So the correlation coefficient is calculated between increases in duration caused by specific risks and project duration. Spearman Rank Order correlation coefficient between risk 3 and project duration equals zero. Why? Because the task “Disorient Barabusa” is not on the critical path. Even if the duration of the task will increase by 80% or 1.6 hours due to the risk and reach 3.6 hours, it will still be less than the duration of Jonny’s tasks: 3 hours +1 hours = 4 hours. It means that risk 3 does not affect project duration at all and the impact of this risk equals 0.
However, the correlation coefficient is not yet the “risk impact”. Here is the problem. Let us assume that our project has only one task “dig treasure” and one risk “Concrete of the parking lot may be stronger than expected”. What would be the correlation coefficient between changes in duration caused by the risk and project duration? The answer is 100%. It means that each time the risk occurs, the duration will increase. Now, what happens if this risk will increases duration not by 20%, but by 90%. The correlation coefficient will be the same. Spearman Rank Order correlation coefficient will be the same if all values are multiplied on one number.
To avoid this problem the following calculation algorithm is used:
1. Calculate correlation coefficient as a result of Monte Carlo simulation as described above
2. Calculate the project duration or cost with and without risks. Project duration with risk is the mean project duration. In our case project duration without risks and mean project duration as a result on Monte Carlo simulations (with risks) equals 4 hours.
3. Calculate the impact coefficient = project duration with risk / (2 * project duration no risks). In our case impact coefficient equals 0.5.
4. Calculated risk impact equals correlation coefficient multiplied on impact coefficient. In our case impacts will be 40%=0.8 * 0.5 * 100% and 0.275=0.55*0.5*100% for risks 1 and 2. Impact of risk 3 will be zero.
Basically, from this we calculate that a risk that leads to a doubling of project duration or 100% has impact 100%. Why two times and not three or five? It is a somewhat arbitrary number, but it allows us to consistently compare the impact of risk across multiple projects.
Finally, we calculate the risk scores as the risk probability multiplied by the risk impact and rank risks based on the risk scores. So in our story, Jonny should receive the greater share of the treasure because based on project duration criteria our pirates choose, his risks have the most potential to increase the project duration.
Two pirates, Jonny Death and Orlando Plume found that a treasure chest was buried beneath the parking lot of the Miami Dolphin’s Stadium and are planning to dig it out in the morning. However, Captain Barabusa suspects that Jonny and Orlando have discovered something and intends to arrive at the parking lot at exactly the same time. But our two clever pirates have a plan; while Jonny excavates the treasure chest, Orlando will attempt to disorient Barabusa by telling him that Jonny is just sewer repair contractor and send Barabusa off in the wrong direction. As part of their plan, they created a project schedule :

The final question is how Jonny and Orlando are going to the treasure. After some discussion, they decide that who assumes the most risk should receive the largest share of the treasure. They also agree, that most important risk is that which has the potential to cause the greatest delay in the project. They identified 3 risks:
Probability Delay of the task this risk is assigned to
1 Concrete of the parking lot may be stronger than expected: Probability=20% Task Delay=20%
2 The chest will be heavier than expected: Probability=20% Task Delay=20%
3 Captain Barabusa may be smarter than expected and it will take longer to disorient him: Probability=90% Task Delay=80%
Based on this risk breakdown structure, Jonny will have to deal with the first two risks, while Orlando with deal with the last one. Orlando argues that he is assuming the most critical (90% chance that this risk will cause 80% delay) and that he deserves greater share of treasure. If we were performing qualitative analysis, where are not assigned to the project schedule, he would absolutely correct. However, in quantitative analysis that use Monte Carlo simulations, the results can be completely be decidedly different..
In quantitative analysis, the impact of risks are calculated based on the correlation between specific changes in duration, cost, or other parameter caused by the risk occurring and and changes in the overall project duration, cost, or other parameters.
Here is how calculation works in our particular example. In each Monte Carlo simulation, changes in duration caused by particular risk are calculated. For example, in simulation 1 due to the risk “Concrete of the parking lot may be stronger than expected” Task 1 experiences a delay of 0.6 hours.
So the correlation coefficient is calculated between increases in duration caused by specific risks and project duration. Spearman Rank Order correlation coefficient between risk 3 and project duration equals zero. Why? Because the task “Disorient Barabusa” is not on the critical path. Even if the duration of the task will increase by 80% or 1.6 hours due to the risk and reach 3.6 hours, it will still be less than the duration of Jonny’s tasks: 3 hours +1 hours = 4 hours. It means that risk 3 does not affect project duration at all and the impact of this risk equals 0.
However, the correlation coefficient is not yet the “risk impact”. Here is the problem. Let us assume that our project has only one task “dig treasure” and one risk “Concrete of the parking lot may be stronger than expected”. What would be the correlation coefficient between changes in duration caused by the risk and project duration? The answer is 100%. It means that each time the risk occurs, the duration will increase. Now, what happens if this risk will increases duration not by 20%, but by 90%. The correlation coefficient will be the same. Spearman Rank Order correlation coefficient will be the same if all values are multiplied on one number.
To avoid this problem the following calculation algorithm is used:
1. Calculate correlation coefficient as a result of Monte Carlo simulation as described above
2. Calculate the project duration or cost with and without risks. Project duration with risk is the mean project duration. In our case project duration without risks and mean project duration as a result on Monte Carlo simulations (with risks) equals 4 hours.
3. Calculate the impact coefficient = project duration with risk / (2 * project duration no risks). In our case impact coefficient equals 0.5.
4. Calculated risk impact equals correlation coefficient multiplied on impact coefficient. In our case impacts will be 40%=0.8 * 0.5 * 100% and 0.275=0.55*0.5*100% for risks 1 and 2. Impact of risk 3 will be zero.
Basically, from this we calculate that a risk that leads to a doubling of project duration or 100% has impact 100%. Why two times and not three or five? It is a somewhat arbitrary number, but it allows us to consistently compare the impact of risk across multiple projects.
Finally, we calculate the risk scores as the risk probability multiplied by the risk impact and rank risks based on the risk scores. So in our story, Jonny should receive the greater share of the treasure because based on project duration criteria our pirates choose, his risks have the most potential to increase the project duration.
Intaver Support Team
Intaver Institute Inc.
Home of Project Risk Management and Project Risk Analysis software RiskyProject
www.intaver.com
Intaver Institute Inc.
Home of Project Risk Management and Project Risk Analysis software RiskyProject
www.intaver.com