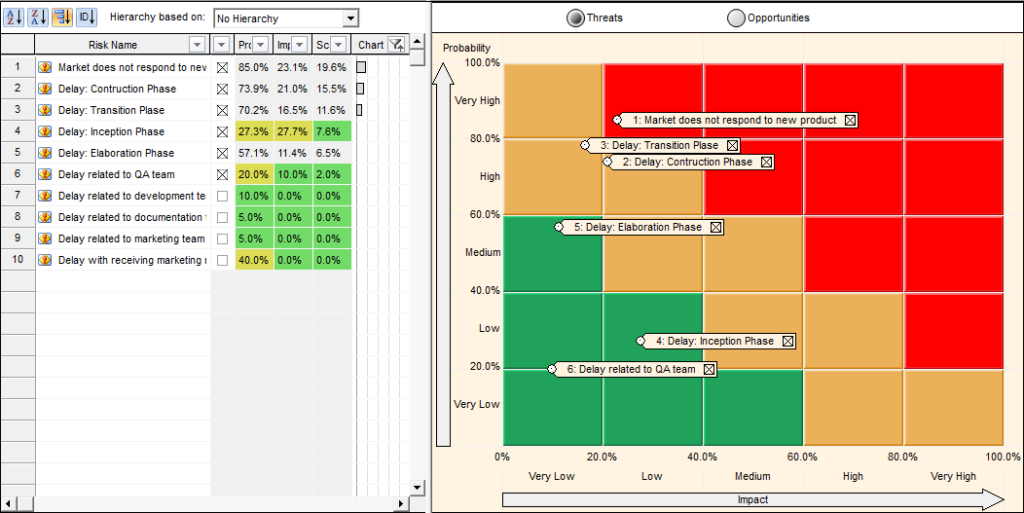
A very common topic of discussion with RiskyProject users is how risks are scored. In most cases, users are familiar with traditional qualitative risk scoring that is a simple probability multiplied by impact. The advantage of this type of scoring is that it is both easy to understand and communicate severity to stakeholders. If you are used to see this type of scoring, RiskyProject ‘s quantitative scoring can appear difficult to comprehend and communicate and you might ask why we don’t use the standard scoring method. To understand why, I’ll first discuss the shortcomings of the standard risk scoring method.
Risk scores are of second order importance when assessing project risks. Primarily, risk assessment is about prioritization and the score should be considered as a value that is used to prioritize how risks will be managed and traditional risk matrix type scoring is notoriously unreliable and can often lead to poor or “worse than random decisions”. This is analogous to how high total cholesterol has been used as a marker for heart disease. Using this as a marker, health authorities developed nutritional guidelines designed to lower cholesterol in the general population that focused on a low fat diet that has resulted in a massive increase in diabetes and obesity. If this was a project, it would viewed in the same light as Napoleon’s invasion of Russia. With this in mind, we can see how important it is ensure what you are measuring is an accurate reflection of the state of your project.
To increase the accuracy and validity of the risk scores and ranking, RiskyProject calculates risk scores based on their measured impact on defined project parameters such as duration or costs. Risk probability and impacts to cost and schedule assigned to project activities and resources. So, in addition to the estimates for probability and impacts, the calculation also takes into account estimates for task durations, costs, and resource allocation. In each iteration, when you run a simulation RiskyProject does two things to calculate risk scores. First, it measures the impact of each risk on each parameter is measured in absolute units (days, dollars, etc). As each risk occurs probabilistically and can have a range of impacts, these impacts can range from 0 – x depending on the parameter measured. Second, the total project cost, duration, finish time, work and success rates are calculated.
From these two measurements, the correlation between each and parameter is calculated. This correlation accurately reflects the expected or probabilistic impact of each risk on each parameter. Using risk weighting, this ranking can be extended to rank risks based on their overall impact on a project. Risk weighting assigns a relative importance of one project outcome over another. For example, if a project a delay in a project will incur substantial penalties or other losses, schedule impacts can be assigned a higher importance for scoring purposes and is included in the risk score when looking at rankings for all parameters.
Communicating the results of this type of analysis can be challenging if your team is expecting to see risks scored as “High” or “20”. A risk score of 32.5% doesn’t elicit the reaction of a risk ranking of severe, highlighted in red. Make your stakeholders aware that the focus of the assessment is not to generate scores, but to prioritize risk planning by accurately ranking of risks based on calculated impacts on project objectives. If that is not enough, it is possible to calculate the expected values of risks in dollars and days, but that is a subject for another post.
The focus of risk assessments needs to be shifted from labels or scores to ranking and prioritization. This requires abandoning or minimizing the use of unreliable qualitative methods and the use of quantitative methods that incorporate risks, cost, and schedule data that provide a more valid basis for decision making.
Figure: Ranking project risks in RiskyProject