About Task and Project Deadlines
Risk analysis helps to determine a task or a project success rate, which could be an important factor in making project decisions. Success Rates are the chance that a task or project can be completed. A task success rate of 56% means that there is a 56% chance that this task or project will be completed and 44% percent chance that task will be canceled. Let’s see how this works in a probabilistic analysis.
If you love action movies, you probably have an appreciation of scenes that involve the defusing of a bomb. Commonly, they tend to feature a scene in which for a few very intense minutes, one of the main characters has to defuse a bomb by selecting which wire to cut and avert a catastrophe. Looking back over the years, some of our favorite bomb defusing scenes include: Juggernaut (1974), where the British government airlifts a Royal bomb disposal squad to a luxury liner to defuse a number of explosive devices; The Shadow (1994) with Alec Baldwin; and, Die Hard with a Vengeance (1995) with Bruce Willis.
What makes these movies so compelling is the deadline: the clock is ticking and if the wires are not cut properly and on time, the hero and any number of innocent victims will disappear with a loud bang. For our purposes, we like to consider these scenes as projects. The duration is uncertain as it is unclear how long it will take to defuse the bomb and an early finish may not always be a positive result! However, barring the hero cutting the wrong wire, all activities must be completed before the timer completes the countdown. In other words, there is a chance that the project will not be completed on time. In this case, it is very important to know the success rate that the project will be complete before the deadline and everything ends badly. While in the movies, the heroes rarely think about such things, in our case, if the success rate is low, we need to find another alternative, reduce probability of risks occurring, or avoid it altogether.
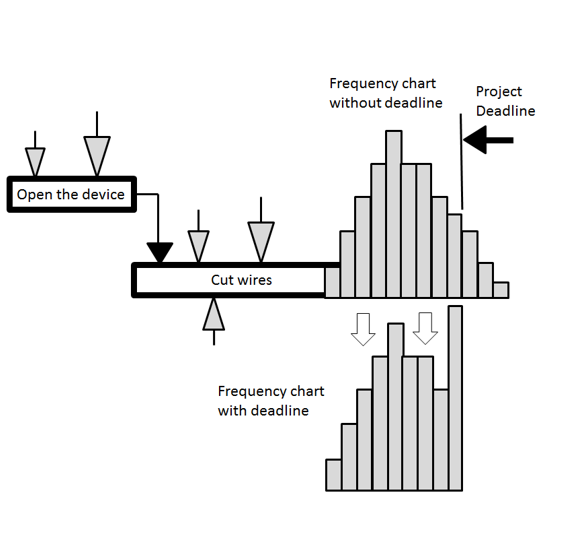
The first thing we need to do is calculate the success rate, which we can do in the following manner. A simple schedule for the project “Defuse the bomb” has two activities: “Open the device” and “Cut wires”, which should take about 1 and 1.5 minutes respectively (see the example below). The project must be completed in 3 minutes; otherwise, the movie will have an unhappy ending. In theory there is enough time to defuse the bomb, however both activities have multiple risks that can delay the project.
To calculate the probabilistic duration and success rate of a project with risk we need to perform Monte Carlo simulations. We will run the simulation and generate the results on the first frequency histogram. From this we can see that in 25% of the iterations, the project duration will be greater than 3 minutes. This converts to a project success rate of 75%. The second (lower) frequency histogram considers that the project duration cannot be greater than 3 minutes regardless of whether the bomb is defused or not. So, in each particular iteration in which duration is greater than 3 minutes, the iteration is set to 3 minutes.
How Deadlines are Defined
Deadlines can affect projects or tasks. If a task reaches a project or task deadline it could cause the following outcomes:
- End task: in this case duration of task will be reduced, but task success rate will not change.
- Cancel task: both success rate and duration will be reduced.
- Reduce success rate: success rate is reduced, but the task duration is not affected.
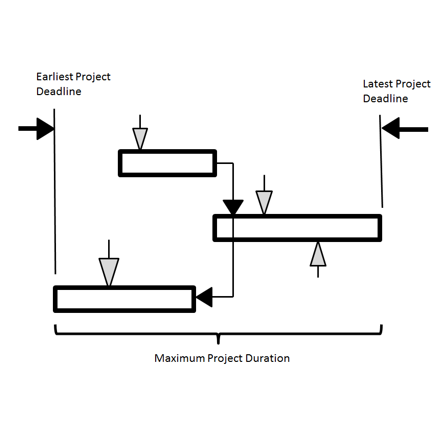
Project deadlines can be defined by earliest deadline, latest deadline and maximum project duration. Earliest deadlines are rare but may occur when these are some combinations of finish to finish or start to finish links between tasks in the project schedule or negative lags.